Longueur de la diagonale d’un parallélépipède rectangle
La longueur d de la diagonale d’un parallélépipède rectangle (ou pavé droit) de longueur L, de largeur l et hauteur h se calcule à partir de la formule suivante :
![]()
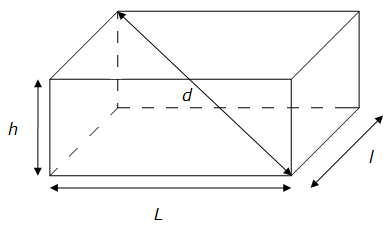
Remarque : les diagonales d’un parallélépipède ont toutes la même longueur.
Principe de calcul de la longueur de la diagonale d’un parallélépipède rectangle
La longueur de la diagonale d’un parallélépipède rectangle se calcule en utilisant deux fois le théorème de Pythagore :
1. On utilise le théorème de Pythagore pour calculer la diagonale d’une des faces du parallélépipède rectangle (ou l’on applique directement la formule de calcul de la longueur de la diagonale d’un rectangle) :
![]()
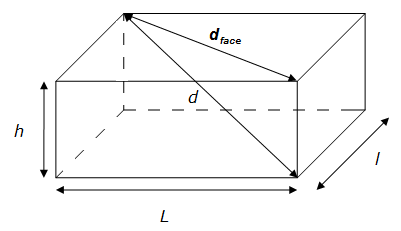
2. On utilise à nouveau la formule de Pythagore pour calculer la longueur de la diagonale du parallélépipède rectangle à partir du résultat précédent. On applique la formule à une hauteur et à la diagonale d’une face pour obtenir la longueur de la diagonale du parallélépipède rectangle (hypoténuse du triangle):
![]()
Exemple
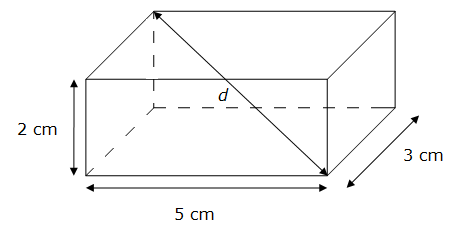
Soit un parallélépipède rectangle de longueur L = 5 cm, de largeur l = 3 cm et de hauteur h = 2 cm.
La longueur d de la diagonale de ce parallélépipède rectangle est égale à :
![]()
Sur le même sujet :
À lire aussi :