Surface et aire d’une couronne circulaire
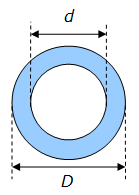
Soit une couronne circulaire de diamètre extérieur D et de diamètre intérieur d. L’aire A de la surface de cette couronne circulaire est calculée à partir de la formule suivante :
A = π/4 (D² – d²)
En considérant R le rayon extérieur de la couronne et r son rayon intérieur, la formule devient :
A = π (R² – r²)
Remarque :
Les deux diamètres ou rayons doivent être données dans la même unité de longueur. L’aire de la couronne circulaire sera alors exprimée dans cette même unité de longueur au carré.
Principe de calcul de l’aire d’une couronne circulaire
Un couronne circulaire est une figure plane délimitée par deux cercles concentriques (i.e. deux cercles ayant le même centre).
La surface de la couronne circulaire correspond à la surface comprise entre ces deux cercles. Pour calculer la valeur de cette aire, il suffit de soustraire l’aire du cercle le plus petit à l’aire du cercle le plus grand.
Sachant que l’aire d’un cercle de rayon r est égale à π r², la formule de calcul de l’aire A d’une couronne circulaire est :
A = π R² – π r² = π (R² – r²)
Ou, en considérant le diamètre extérieur D et le diamètre intérieur d de la couronne :
A = π ((D/2)² – (d/2)²) = π/4 (D² – d²)
En mécanique le calcul de l’aire d’une couronne circulaire permet de calculer la surface de contact d’une rondelle plate.
Exemple de calcul
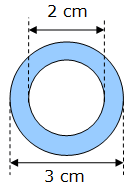
Soit une couronne circulaire dont le diamètre extérieur est de 3 cm et le diamètre intérieur de 2 cm. L’aire A de la surface de cette couronne est égale à :
A = π/4 (3² – 2²) ≈ 3,927 cm²
Sur le même sujet :
À lire aussi :