LeMemento.fr

Soit une sphère de rayon R. On calcule le rayon r d’une section de cette sphère dont le centre est distant de H du centre de la sphère à partir de la formule suivante :

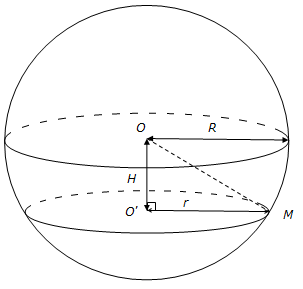
Principe de calcul du rayon d’une section plane d’une sphère

Dans le schéma ci-dessus :

• La sphère a pour centre le point O, et la valeur de son rayon vaut R.
• La section de la sphère a pour centre O’, et son rayon (dont on cherche à calculer la valeur) est égal à r.
• La distance séparant O et O’ est égale à H.
• M est un point d’intersection entre la sphère et la section dont on cherche à calculer le rayon r.

On constate que :

• La distance séparant les poins O et M est égale au rayon R de la sphère puisque M est un point de la sphère.
• La distance séparant O’ et M est égale à r, puisque M appartient aussi à la section de la sphère dont on cherche à calculer le rayon.
• Les points O, O’ et M forment un triangle rectangle en O’.

En appliquant le théorème de Pythagore sur le triangle rectangle formé par les point O, O’ et M on obtient :

Remarque :

R et H doivent être exprimés dans la même unité de longueur. La valeur calculée pour le rayon r sera alors exprimée dans cette même unité.

Exemple

Soit une sphère dont le rayon R est égal à 2 cm, et une section plane de cette sphère dont le centre est à 1 cm du centre de la sphère. Le rayon r de cette section de la sphère est égal à :