Longueur d’un arc de cercle
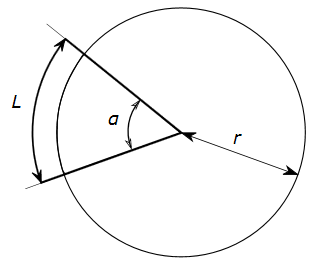
Un arc de cercle (ou segment circulaire) est une partie de la circonférence d’un cercle. Il est défini par le rayon r du cercle auquel il appartient et par l’angle α (alpha) du secteur angulaire qui le défini.
La formule permettant le calcul de la longueur L d’un arc de cercle dépend de l’unité dans laquelle l’angle α est exprimé.
Si l’angle α est exprimé en radians :
L = αr
Si l’angle α est exprimé en degrés :
L = απr/180
Si l’angle α est exprimé en grades :
L = απr/200
Remarques :
- La longueur L d’un arc de cercle est exprimée dans la même unité de longueur que le rayon r. Par exemple si le rayon est exprimé en centimètres, la longueur de l’arc de cercle sera elle aussi exprimée en centimètres.
- Dans un cercle de rayon 1, la longueur d’un arc de cercle est égale à la valeur de son angle en radians.
Principe de calcul de la longueur d’un arc de cercle
Par définition, le nombre π est le rapport entre la circonférence d’un cercle et son diamètre :
circonférence du cercle = 2πr
Avec l’angle α exprimé en radians on a également la relation :
L / circonférence = α/2π
En substituant la circonférence, on obtient la formule de calcul de la longueur d’un arc de cercle avec un angle α exprimé en radians :
L / 2πr = α/2π <=> L = αr
La conversion entre radians et degrés est calculée par la formule :
radians = degrés . π / 180
Par conséquent, la longueur d’un arc de cercle avec un angle exprimé en degrés est égale à :
L = απr/180
La conversion entre radians et grades est calculée par la formule :
radians = grades . π / 200
Par conséquent, la longueur d’un arc de cercle avec un angle exprimé en grades est égale à :
L = απr/200
Exemple
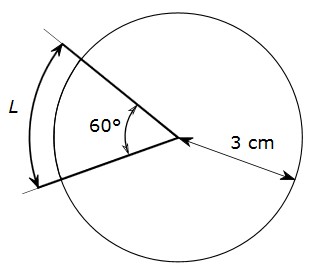
Soit un cercle de rayon r = 3 cm et un arc de cercle défini par un angle α de 60°. La longueur L de cet arc de cercle est égale à :
L = απr/180 = 180π/180 = π cm
Sur le même sujet :
À lire aussi :