Calcul de l’aire d’un triangle sans connaître sa hauteur
Comment calculer l’aire d’un triangle sans connaître sa hauteur ?
L’aire S de la surface d’un triangle quelconque dont la hauteur est h et la longueur de la base est a se calcule à partir de la formule de base suivante :
S = ah / 2
Dans le cas de triangles particuliers, les formules de base permettent de calculer leur aire sans connaître leur hauteur h :
L’aire d’un triangle quelconque peut être calculée sans connaître sa hauteur à partir de la formule de Héron (du nom du mathématicien grec Héron d’Alexandrie) ou de la loi des sinus.
Soit un triangle quelconque défini par trois points A, B et C :
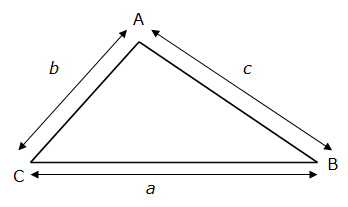
Les angles du triangle sont définis comme suit :
- Angle en A : α
- Angle en B : β
- Angle en C : γ
Calcul de l’aire d’un triangle avec la formule de Héron
Le périmètre P d’un triangle est défini par la formule :
P = a + b + c
La formule de Héron permet de calculer l’aire d’un triangle quelconque à partir de son demi-périmètre p :
p = P / 2
![]()
Calcul de l’aire d’un triangle à partir de la loi des sinus
La loi des sinus spécifie que dans un triangle :
a / sin(α) = b / sin(β) = c / sin(γ)
Si on connaît la valeur d’un angle et la longueur des deux côtés adjacents, l’aire S du triangle peut se calculer à partir de la formule :
S = ab.sin (γ) / 2 = bc.sin(α) / = ac.sin(β)
Si on connaît la longueur d’un côté et la mesure des deux angles adjacents, l’aire S du triangle peut se calculer à partir de la formule :
S = a² sin(β) sin (γ) / (2 sin(β + γ))
Sur le même sujet :
À lire aussi :