Volume d’un cône
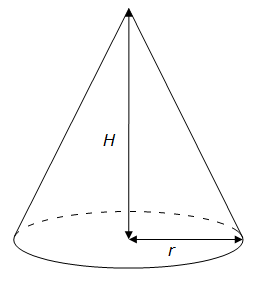
Le volume d’un cône de révolution est égal à un tiers de l’aire de sa base, multiplié par la hauteur H du cône.
L’aire de la base du cône de rayon r est égal à π x r².
La formule de calcul du volume V d’un cône de révolution de rayon r et de hauteur H est donc :
V = π r² H / 3
Calculer le volume d’un cône de révolution
Pour calculer le volume d’un cône de révolution, entrez le rayon de sa base et sa hauteur dans le calculateur ci-dessous. L’aire du disque qui correspond à la base du cône et le volume du cône s’affichent avec une précision de 10 chiffres après la virgule.
| Résultats : | ||
|---|---|---|
| Aire de la base du cône : | ??? | u² |
| Volume du cône : | ??? | u³ |
Pour calculer le volume d’un cône, son rayon r et sa hauteur H doivent être exprimés dans la même unité de longueur (notée u dans le tableau ci-dessus). Le volume du cône sera alors exprimé dans cette même unité au cube. Par exemple, si le rayon et la hauteur du cône sont exprimés en cm, le volume calculé sera exprimé en cm³.
Le volume d’un cône est égal à 1/3 du volume du cylindre ayant le même rayon et la même hauteur. Il est donc le produit de l’aire du disque qui correspond à la base du cône multiplié par la hauteur du cône et divisé par 3.
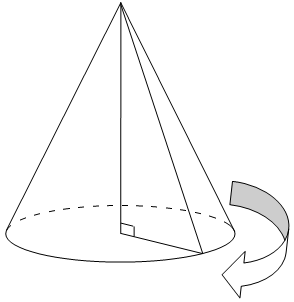
Un cône de révolution est généré lorsque l’on fait pivoter de 360° un triangle rectangle autour de l’un des côtés de l’angle droit :
- La base du cône de révolution est un disque.
- La hauteur du cône est la distance entre le centre du cercle qui délimite sa base et son sommet.
- La surface latérale du cône est engendrée par l’hypoténuse du triangle rectangle que l’on fait pivoter.
- Les segments reliant le sommet du cône et n’importe que point du cercle délimitant sa base sont appelés génératrices du cône et ont tous la même longueur.
Exemple de calcul du volume d’un cône
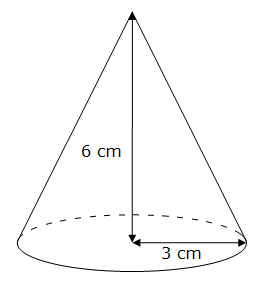
Soit un cône dont la hauteur est de 6 cm et dont la base a un rayon de 3 cm. Le volume V de ce cône est égal à :
V = π x 3² x 6 / 3 ≈ 56,55 cm³
Sur le même sujet :
À lire aussi :