Volume d’une pyramide à base carrée
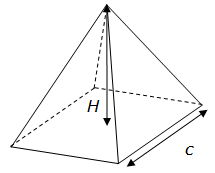
Le volume d’une pyramide régulière est égal à la surface de sa base multiplié par sa hauteur et divisé par 3. Dans le cas d’une pyramide à base carrée de hauteur H et dont la longueur de chaque côté de la base vaut c, la formule de calcul du volume V de cette pyramide est la suivante :
V = c² x H / 3
Calcul du volume d’une pyramide à base carrée
Pour calculer le volume d’une pyramide à base carrée, entrez la longueur de chaque côté de sa base et sa hauteur dans le calculateur ci-dessous. L’aire du carré qui correspond à la base de la pyramide et le volume de la pyramide s’affichent avec une précision de 10 chiffres après la virgule.
| Résultats : | ||
|---|---|---|
| Aire de la base de la pyramide : | ??? | u² |
| Volume de la pyramide : | ??? | u³ |
Pour calculer le volume d’une pyramide, sa hauteur H et la longueur c de chaque côté doivent être exprimées dans la même unité de longueur (notée u dans le tableau ci-dessus). Le volume de la pyramide sera alors exprimé dans cette même unité au cube. Par exemple, si la longueur du côté et la hauteur de la pyramide sont exprimés en cm, le volume calculé sera exprimé en cm³.
Une pyramide à base carrée est un polygone régulier : le sommet de la pyramide est à la verticale du centre de gravité de la base (point d’intersection des diagonales du carré).
Les 4 côtés d’une pyramide à base carrée sont des triangles isocèles.
Exemple
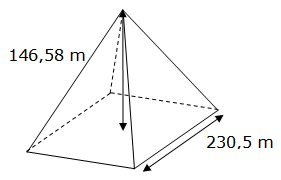
La pyramide de Khéops à Gizeh est une pyramide carrée dont la hauteur initiale était de 148,58 m et dont la longueur moyenne des côté est de 230,5 m (source wikipedia). Le volume V de cette pyramide est égal à :
V = 230,5² x 146,58 / 3 = 2 595 944,015 m³
Sur le même sujet :
À lire aussi :