LeMemento.fr

Soit un triangle quelconque dont la hauteur est égale à h et la longueur de la base est L. L’aire A de ce triangle est égale à :

A = L x h / 2

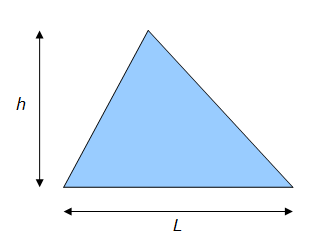
Principe de calcul de l’aire d’un triangle quelconque

En traçant une hauteur d’un triangle quelconque (droite passant par un sommet du triangle et perpendiculaire au côté opposé à ce sommet) , on décompose ce triangle en deux triangles rectangles.

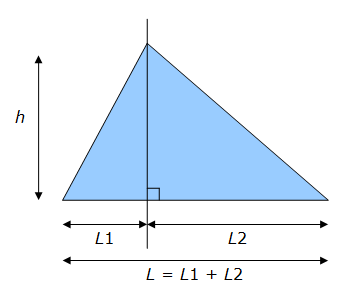
L’aire de la surface du triangle quelconque est égale à la somme des aires des deux triangles rectangles, soit en reprenant le principe du calcul de l’aire d’un triangle rectangle :

A = h x L1 / 2 + h x L2 / 2

Soit en factorisant par h / 2 :

A = (L1 + L2) x h / 2

Et comme L1 + L2 = L :

A = L x h / 2

Remarque : la hauteur du triangle peut être calculée à partir du théorème de Pythagore si l’on connaît L1 ou L2 ainsi que les longueurs des côtés du triangle quelconque.

Exemple 1

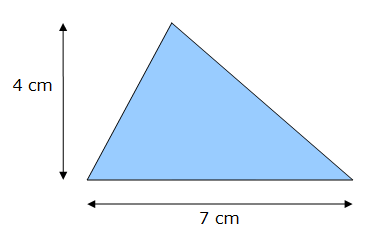
Soit un triangle de hauteur h = 4 cm et dont la longueur de la base est de L = 7 cm. L’aire A de ce triangle est égale à :

A = L x h / 2 = 7 x 4 / 2 = 14 cm²

Exemple 2

Soit un triangle de hauteur h = 4 cm et dont la longueur de la base est de L = 5 cm. L’aire A de ce triangle est égale à :

A = L x h / 2 = 5 x 4 / 2 = 10 cm²

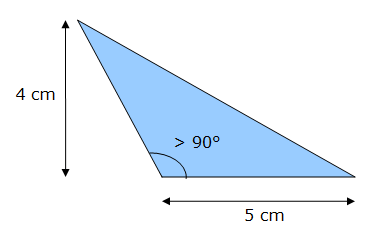
Remarque : dans le cas d’un triangle obtus, obtusangle ou ambligone (un des angles du triangle est supérieur à 90°), la formule s’applique également. Simplement dans le principe expliqué ci-dessus, L1 aurait une valeur négative et L2 une valeur supérieure à L. Dans le principe on soustrait les deux aires des triangles rectangles au lieu de les additionner.