Aire et surface d’un triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés sont égaux. Si a est la longueur de ces trois côtés, l’aire A correspondant à la surface de ce triangle équilatéral est égale à :
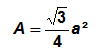
Un triangle équilatéral ayant les propriétés d’un triangle quelconque, si h est la hauteur du triangle équilatéral, son aire A est égale à :
A = a x h / 2
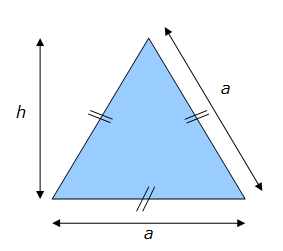
Principe de calcul de l’aire d’un triangle équilatéral
Un triangle équilatéral est un triangle dont les trois côtés ont la même longueur. Dans un triangle équilatéral, la médiatrice forme un angle droit avec une base qu’elle coupe en son milieu.
Le triangle équilatéral se décompose donc en deux triangles rectangles symétriques.
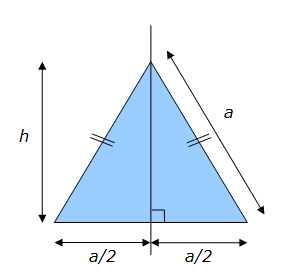
En appliquant le théorème de Pythagore à l’un de ces triangles on obtient :
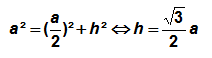
Le triangle équilatéral est aussi un triangle quelconque et hérite de ses propriétés. On a donc :
A = a x h / 2
En remplaçant h dans cette équation, on obtient finalement :
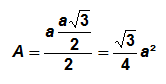
Exemple
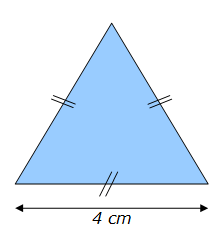
Soit un triangle équilatéral dont chaque côté mesure 4 cm. La surface de son aire A est égale à :
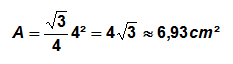
Sur le même sujet :
À lire aussi :