LeMemento.fr

Soit un losange dont la longueur des côtés est égale à c, la hauteur est égale à h, et la longueur des deux diagonales valent d1 et d2. L’aire A de la surface de ce losange peut se calculer à partir de deux formules / méthodes distinctes  :

A = c x h

ou

A = d1 x d2 / 2

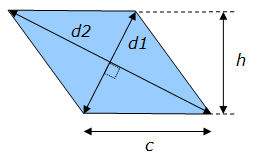
Principe de calcul de l’aire d’un losange

Par définition, tous les côtés du losange ont la même longueur, et un losange peut se décomposer en deux triangles symétriques :

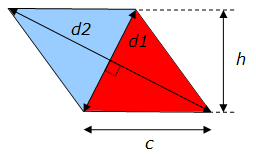
L’aire de la surface d’un triangle est le produit de la base de ce triangle par sa hauteur divisé par 2. On a donc :

• Aire du triangle bleu = Aire du triangle rouge
• Aire du triangle bleu = c x h / 2
• Aire du triangle rouge = (d1 x d2 /2) /2 = d1 x d2 / 4

Étant donné que la surface du losange équivaut à deux fois l’aire d’un triangle de base (triangle bleu ou rouge), l’aire de la surface A du losange est égale à :

A = (c x h / 2) x 2 = c x h

ou

A = (d1 x d2 / 4)  x 2 = d1 x d2 / 2

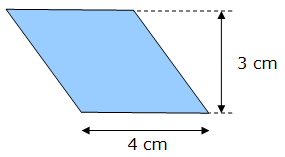
Exemple 1 : calcul à partir de la hauteur du losange

Soit un losange dont la longueur des côtés est de 4 cm et la hauteur est de 3 cm. L’aire A de la surface de ce losange est égale à :

A = 3 x 4 = 12 cm²

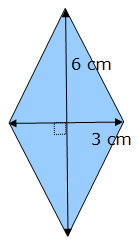
Exemple 2 : calcul à partir de la longueur des diagonales du losange

Soit un losange dont la mesure des diagonales est de 6 cm et 3 cm. L’aire A de la surface de ce losange est égale à :

A = 6 x 3 / 2 = 9 cm²