LeMemento.fr

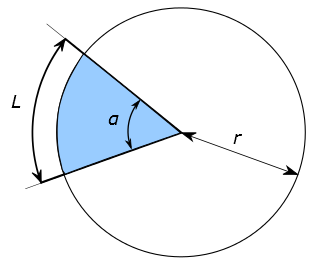
Un secteur circulaire est une partie ou portion de disque définie par un angle (en bleu dans le dessin ci-dessous).

Soit un secteur circulaire défini par un angle α. L est la longueur de l’arc de cercle correspondant à ce secteur circulaire. L’aire A correspondant à la surface du secteur circulaire peut-être calculée à partir des formules suivantes :

Si l’angle α est exprimé en radians :

A = αr² / 2

Si l’angle α est exprimé en degrés :

A = παr² / 360

Si l’angle α est exprimé en grades :

A = παr² / 400

A partir de la longueur L de l’arc de cercle correspondant au secteur circulaire :

A = Lr / 2

Remarques :

• L’aire du secteur circulaire est exprimée dans l’unité du rayon au carré. Par exemple, si le rayon est exprimé en centimètres (cm), l’aire du secteur circulaire sera exprimé en cm².
• Si le calcul est effectué à partir de la longueur L de l’arc de cercle correspondant au secteur circulaire, cette longueur et le rayon doivent être exprimés dans la même unité. L’aire du secteur circulaire sera alors exprimée dans cette unité au carré.

Principe de calcul de l’aire d’un secteur circulaire

L’aire d’un disque de rayon r est égale à :

A = πr²

L’aire du secteur circulaire est directement proportionnel à son angle α. Donc en fonction de l’unité d’angle utilisée pour α :

• Pour un angle exprimé en radians (le cercle complet correspond à 2π) :

A = πr² .  α/2π = αr²/2

• Pour un angle exprimé en degrés (le cercle complet correspond à 360°) :

A = πr² .  α/360 = παr²/360

• Pour un angle exprimé en grades (le cercle complet correspond à 400 grades) :

A = πr² .  α/400 = παr²/400

Calcul à partir de la longueur de l’arc de cercle (portion de cercle) correspondant au secteur circulaire

Pour un angle exprimé en radians, la longueur L de l’arc de de cercle est égale à :

L = αr

En remplaçant αr dans la formule de calcul de l’aire d’un secteur circulaire avec une angle exprimé en radians on obtient :

A = αr²/2 = Lr / 2

Exemple de calcul à partir de l’angle

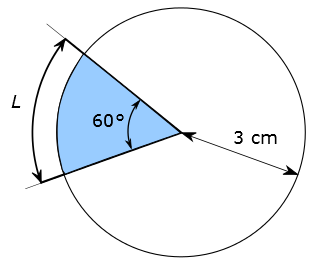
Soit un secteur circulaire défini dans un cercle de rayon 3 cm et par un angle de 60°. L’aire A de ce secteur circulaire est égale à :

A = π. 60 . 3² / 360 = 540π/360 = 3π/2 ≈ 4,71 cm²