Surface et cercle : aire d’un disque
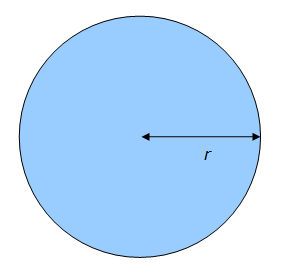
La surface délimitée par un cercle de rayon r correspond à l’aire A du disque de rayon r.
L’aire A d’un disque de rayon r est égale à :
A = π r ²
En considérant le diamètre d du cercle plutôt que son rayon la formule devient :
A = π d ² / 4
Remarque :
Un cercle de centre O et de rayon r est défini par tous les points dont la distance avec le point O est égale au rayon r du cercle. Les points du cercle dessinent sa circonférence.
Le disque correspondant à ce cercle inclue l’ensemble des points inscrits dans ce cercle et sur sa circonférence.
Le terme surface ou aire d’un disque est donc plus approprié que le terme surface ou aire d’un cercle.
Exemple de calcul de la surface d’un disque
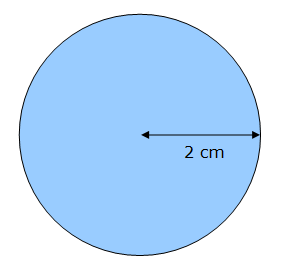
Soit un disque délimité par un cercle de rayon r = 2 cm.
L’aire A de ce disque est égale à :
A = π r ² ≈ 3,14 x 2² ≈ 12,56 cm²
Sur le même sujet :
À lire aussi :