LeMemento.fr

Théorème de Pythagore : dans un triangle rectangle, le carré de l’hypoténuse est égal à la somme des carrés des longueurs des côtés de l’angle droit.

c² = a² + b²

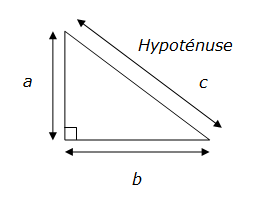
L’hypoténuse est le côté opposé à l’angle droit. Les deux autres côtés sont appelés cathètes.

Comme le carré de la longueur de l’hypoténuse est égal à la somme des carrés des longueurs des deux autres côtés, l’hypoténuse est toujours le côté le plus long du triangle rectangle.

La réciproque du théorème de Pythagore est également vraie : si dans un triangle, le carré de la longueur du plus grand des côtés est égal à la somme des carrés des deux autres côtés, alors ce triangle est un triangle rectangle. Le côté le plus long de ce triangle rectangle est son hypoténuse, et l’angle opposé est un angle droit.

Le théorème de Pythagore permet de calculer par exemple la diagonale d’un rectangle ou d’un carré, il est aussi à la base du calcul de l’aire d’un triangle.

Si le rapport entre la longueur de l’hypoténuse d’un triangle rectangle et les longueurs des deux autres côté semble être déjà connue par les  babyloniens vers 1700 av J.C, c’est les principes établis par le philosophe grec Pythagore ( ≈ 580 – †495 av J.C) qui permettront d’en faire la démonstration. En plus des mathématiques, Pythagore s’intéresse à la philosophie, la musique, l’éthique, la politique, l’astronomie (il sera le premier à appeler le ciel cosmos et à dire que la terre est ronde).

Exemple

Soit un triangle rectangle dont la longueur de l’hypoténuse c est de 5 cm. Les deux autres côtés ont des longueurs a et b de respectivement 3 cm et 4 cm.

c² = a² + b² => 5² = 3² + 4² = 25 cm

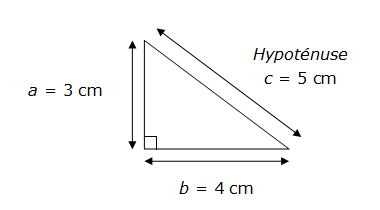
Les dimensions 3-4-5 correspondent à la plus petite mesure d’un triangle rectangle avec des nombres entiers pour longueurs des côtés. Elles sont à la base d’une corde à treize noeuds utilisée jusqu’à la fin du moyen âge et qui permettait aux géomètres de tracer des triangles rectangles.